This is Part 7 in a series of posts discussing Cost of Delay and making objective decisions in new product development, based on economic analysis.
In this part, we discuss how to calculate the economic value of a decision quantitatively, and how to account for uncertainty in the economic variables we change with each decision.
In this part, Part 7, we discuss how to calculate the Economic Value of a decision quantitatively, and how to account for uncertainty in the economic variables we change with each decision.
Calculating economic decision value (expected profit)
As in Moneyball, the game changer at our fingertips is the ability to quantify Value mathematically. The unit of measure we use is dollars-profit. "You are what you measure," and measuring the profitability of your decisions increases profitability.
We will use the same examples we've discussed previously to build an understanding of Economic Value calculations and how to accommodate uncertainty in new product development projects. Assume the Economic Sensitivities and Cost of Delay shown below are based on the mean forecast. After eliminating the impact of uncertainty in these as discussed in post 6, we will consider these a given.
To avoid any confusion with sales Volume (V) and sales Price (P), we will use the term Economic Value or Expected Value (EV) for the incremental value or profit we expect from a decision. We'll use these terms interchangeably to make the point that is it both - expected and economic. It is very similar to Expected Monetary Value as described well in books by Don Reinertsen and others, but we are going to look at things a little bit differently, especially in the next post, so we will use Expected Value to distinguish it.
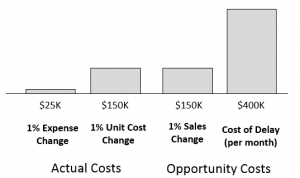
Figure 1: Example Economic Sensitivities
Example 1: Economic value of expediting parts
Recall from the first example in post 5 that by expediting a part (Part A) for $5K we could save one day on our schedule at a $20K/day Cost of Delay. This increases our profit by $15K. The simple Economic/Expected Value (EV) is the Gain (G) minus the Cost (C). The gain in this case is the amount of delay (∆D ) times the Cost of Delay ($20K/day).
EV = G – C = COD * ∆D - C
EV = $20K/day * 1 day – $5K = $15K
And the simple Decision ROI is the Economic Value (EV) divided by the Cost (C).
ROI = EV / C = (G - C) / C
ROI = $15K / $5K = 3-to-1
Incorporating all economic variables
In our project decisions, there may be gains or costs from changes to any of five Economic Variables - Launch Date, Sales Volume, Average Sales Price, Unit Cost, and Expenses. We impact two or more of these variables with any given decision. It is these variables which we are trading off.
For example, we may gain sales volume but incur a cost of delay, by incorporating a few more features. We may gain by reducing unit cost and producing a cheaper product, resulting in a cost in reduced sales volume. We can even gain (save) project expenses by incurring costs in delay or sales volume or unit cost. Any variable can result in a gain or a cost.
If the decision involves long-term changes to the variables, where the decision will impact the variable equally from the first day of launch to the Value Horizon, we can use a simple formula to calculate the Economic Value. For example, if we expect an increase in sales volume or unit cost which will span the life of the product, the profit increase from that decision is an easy calculation.
EV = SVS * ∆V + SPS * ∆P - COD * ∆D - UCS * ∆C - ∆E
Where:
SVS, SPS, COD, and UCS are Sales Volume Sensitivity, Sales Price Sensitivity, Cost of Delay, and Unit Cost Sensitivity, respectively. These are the constants in the equation.
The other terms (∆x) are what we refer to as the Economic Variables.
∆V = Increase in Volume (decreases are negative)
∆S = Increase in Sales Price (decreases are negative)
∆D = Launch Delay (earlier than current date is negative)
∆C = Increase in Unit Cost (decreases are negative)
∆E = Additional Project Expenses (savings are negative)
In the first example, our gain was in having a negative Launch Delay (∆D = -1 day). The cost was in additional Project Expenses (∆E = $5K). The other variables (∆V, ∆S, and ∆C) are zero, because they are not being changed.
EV = 0 + 0 - (20K/day * -1 day) - 0 - $5K = $15K
When calculating ROI, we divide the Economic Value by the additional project expenses we incur with the decision:
ROI = EV / ∆E
ROI = $15K / $5K = 3-to-1
Notice, the Opportunity Costs we incur - Delay Cost, increased Unit Cost, and reduced Sales Price or Volume - are taken into account within the calculation of EV, but are not included as costs in the denominator of the ROI calculation. Thus, ROI is a measure of Opportunity vs Expense.
As mentioned earlier, this formula applies when our decisions and changes impact the product from the first day of launch to the Value Horizon. When changes and decisions impact a significantly smaller portion of that time period, a simple Project Economic Model spreadsheet is used to determine the Economic Value of these decisions. If you would like to build your Project Economic Model spreadsheet using one of our templates, please let me know.
Tackling uncertainty in economic decisions
I know some of you are asking, “How do you know it will actually save one day? How do you know expediting the part will actually save you any time at all?”
The answer is simple. You don’t. That is, you usually don’t know for sure whether it will save any time, or exactly how much time it will save.
Sometimes we do, or at least we have high confidence in our estimate. For example, if we know Part A is the only part we are waiting on and it is truly on the critical chain, and we know our supplier will work the weekend for that extra $5000 we pay them, so we will most likely have it Monday instead of Tuesday, then we can have high confidence that it will save one day.
However, what if we are waiting on two parts? Say there is a 50% chance that the other part (Part B) won’t be here until Tuesday. Then there is only a 50% chance that expediting Part A will save us 1 day. We call this 50% chance our Probability of Success and it lowers the expected gain from making this decision. For these cases, a simple Expected Monetary Value (EMV) calculation can be used to determine the Economic Value.
EV = EMV = Probability of Success * Gain - Cost
EV = 50% * $20K - $5K = $10K – $5K = $5K
And the Expected Return on Investment (EROI) for that decision is:
EROI = EMV / Cost
= $5K / $5K = 1-to-1
The EROI (probability-weighted ROI) is much lower compared to the 3-to-1 ROI if our expedited part was clearly critical.
Multiple decisions required
Notice, the expected gain is ½ day. However, we will actually realize either no gain or a one day gain. There will be no ½ day gain. There is just a 50% probability of a one day gain. The next time we make this bet we may get no gain. Over time, and multiple analyses, the average will reflect the results of our EMV calculations.
This is why we discuss, in the Moneyball post, the law of large numbers and using statistics to achieve gains in the uncertain world of Product Development. Calculating and using Expected Value over multiple decisions is how we increase our average decision value and overall profitability.
Unfortunately, because there are gains and costs across so many different variables, it is not always straight forward and easy to determine exactly what our total cost will be, or what gains we will actually achieve and what our probability of success is. In order to analyze all types of scenarios and decisions, we recommend using a quick best/worst case or simple probability analysis. Please see the next post for a deeper discussion and examples of using these techniques in analyzing our profit-making decisions. Stay tuned...
Want to know how to calculate the cost of delaying your product launch. It could be worth millons of dollars in profit. This free eBook will show you how.
In Part 1, we learn many applications for Cost of Delay analysis, and why it can help improve product development velocity and increase profits.
In Part 2, we define Cost of Delay generally and then talk specifically about its application in product development and see it represented graphically.
In Part 3, we learn how to quickly estimate the Cost of Delay of a product development project.
In Part 4, we discuss how to quickly estimate the other terms generally required to perform a quick economic analysis.
Part 5 shares examples of how to calculate the cost of delay and the subsequent ROI of making some common project trade-offs such as adding a new product feature, and adding resources to an existing project.
Part 6 discusses some important factors to consider when implementing a project economic model and how to manage uncertainty in regards to some key inputs such as sales forecast and unit cost.
Then we took a little intermission to discuss how Economic Decision Making and the movie Moneyball are related, and how important it is to have quantitative assessments of Value.
In Part 8, we discuss how to communicate and account for uncertainty in each decision's impact on launch date, sales volume, and the other Economic Variables.
In Part 9, we discuss how to increase certainty in our economic decisions, in part by increasing the accuracy of our impact estimates.
In Part 10, we discuss some critical success factors for successfully Implementing Project Economic Modeling and Economic Decision Making.
Editor's note: This post was originally published in 2015 and has been updated for accuracy and comprehensiveness.



